Röntgen, Abtasten oder Blutuntersuchungen: Es gibt viele Arten von Tests, die dabei helfen, eine Krankheit zu diagnostizieren. Doch diese Tests liefern nicht ohne weiteres ein „Ja“ oder „Nein“ als Antwort. Oftmals muss aus einem Testergebnis erst die Wahrscheinlichkeit errechnet werden, mit der eine bestimmte Person tatsächlich krank ist oder auch nicht.
Diagnostische Tests liefern Hinweise darauf, ob eine Krankheit vorliegt oder nicht. Um ein Testergebnis einordnen zu können, braucht ein Arzt oder eine Ärztin weitere Informationen über die getestete Person und auch über die Eigenschaften des verwendeten Tests. Erst wenn genügend Informationen verfügbar sind, kann eine sichere Diagnose gestellt werden.
Ist es wahrscheinlich, krank zu sein?
Es klingt paradox, doch um die Wahrscheinlichkeit für eine bestimmte Krankheit zu berechnen, muss man die Wahrscheinlichkeit kennen, mit der diese bestimmte Erkrankung überhaupt auftreten kann. Ein einfaches Beispiel: Bei einem Patienten, der sich in Mitteleuropa mit Fieber einer Ärztin vorstellt, ist es relativ unwahrscheinlich, dass er Malaria hat. Teilt er der Ärztin aber mit, dass er kürzlich von einer Reise aus den Tropen zurückkam, muss bei ihm die Diagnose Malaria in Betracht gezogen werden.
Man spricht hier von Krankheitsprävalenz: Wie oft kommt eine bestimmte Krankheit in einer bestimmten Region oder einer bestimmten Bevölkerungsgruppe durchschnittlich vor, und wie wahrscheinlich ist es demnach für eine individuelle Person, daran erkrankt zu sein?
Wie gut ist der Test? Sensitivität und Spezifität
Wahrscheinlichkeiten spielen aber nicht nur auf der Patientenseite eine Rolle. Auch ein diagnostischer Test erkennt eine vorhandene Krankheit nur mit einer bestimmten Wahrscheinlichkeit. Mit einer Ultraschalluntersuchung – auch das ist ein diagnostischer Test – wird es beispielsweise nicht bei allen Personen mit Schmerzen im Unterbauch gelingen, eine akute Blinddarmentzündung sicher zu bestätigen oder auszuschließen. In einigen Fällen muss eine weitere Untersuchung wie zum Beispiel eine Computertomographie durchgeführt werden, um eine Diagnose zu stellen.
Die Wahrscheinlichkeit, mit der ein Test eine vorhandene Krankheit auch tatsächlich erkennt, ist die sogenannte Test-Sensitivität. Hat beispielsweise ein HIV-Test eine Sensitivität von 99,9 Prozent, bedeutet das, dass bei 99,9 Prozent oder 999 von 1.000 tatsächlich Erkrankten das Ergebnis eines Bluttests positiv ausfällt. In der Fachsprache wird das „richtig positives“ Testergebnis genannt, da der Test die vorhandene Infektion aufgespürt hat. Eine Trefferquote von 99,9 Prozent bedeutet aber auch, dass 0,1 Prozent – oder 1 von 1.000 Erkrankten – fälschlicherweise ein negatives Testergebnis bekommt: ein „falsch negatives“ Testergebnis.
Umgekehrt gibt es für Gesunde, die sich einem Test unterziehen, eine bestimmte Wahrscheinlichkeit, dass der Test bestätigt, dass keine Erkrankung vorliegt: die sogenannte Test-Spezifität – die Wahrscheinlichkeit, dass Gesunde ein korrektes, weil negatives Testergebnis erhalten.
Hat ein HIV-Test eine Spezifität von 99 Prozent, erhalten 99 von 100 Gesunden auch ein negatives Testergebnis (ein „richtig negatives“ Testergebnis). Aber eine gesunde Person wird fälschlicherweise positiv getestet (was im Falle eines HIV-Tests anhand einer zweiten Blutprobe noch einmal überprüft wird, sodass keine falsche Diagnose kommuniziert wird).
Falsch positive Testergebnisse lassen sich nicht vermeiden. Eine hohe Test-Sensitivität („die Kranken entdecken“) geht immer zu Lasten der Spezifität („die Gesunden entdecken“) und umgekehrt. Im Falle von HIV ist es wichtiger, möglichst viele Kranke zu identifizieren, um zu vermeiden, dass sich die Krankheit weiter verbreitet. Deshalb wird beim HIV-Test eine höhere Sensitivität gegenüber der Spezifität vorgezogen (auch wenn die Unterschiede nur sehr gering sind).
Positive und negative Vorhersagewerte – noch mehr Wahrscheinlichkeiten
Kennt die Ärztin nun das Testergebnis und die Wahrscheinlichkeit ihres Patienten, eine bestimmte Krankheit zu haben, kann sie nun endlich die Wahrscheinlichkeit berechnen, mit der der Patient entweder – wie im Beispiel – tatsächlich mit HIV infiziert ist (bei positivem Testergebnis) oder nicht mit HIV infiziert ist (bei negativem Testergebnis). Dazu bedient sie sich einer statistischen Formel, in die die Wahrscheinlichkeit des Patienten, infiziert zu sein (die „Krankheitsprävalenz“), die Test-Sensitivität sowie die Test-Spezifität eingehen. Der so errechnete positive Vorhersagewert ist die Wahrscheinlichkeit des Patienten, tatsächlich infiziert zu sein.
Jemand aus der Allgemeinbevölkerung beispielsweise wird unter der Annahme eines geringen Krankheitsrisikos auf HIV getestet, da die Prävalenz für die Erkrankung in der Allgemeinbevölkerung in Deutschland beispielsweise bei nur 0,1 Prozent liegt. Der berechnete positive Vorhersagewert liegt dann bei 0,09 (die Formeln zur Berechnung stehen am Ende des Textes). Das bedeutet: Bei einem positiven Testergebnis ist diese Person mit einer 9-prozentigen Wahrscheinlichkeit tatsächlich mit HIV infiziert. Gehört der oder die Getestete hingegen einer HIV-Hochrisikogruppe mit einer Krankheitsprävalenz von 10 Prozent an, läge der berechnete positive Vorhersagewert bei 0,92. Was bedeutet, bei einem positiven Testergebnis ist der oder die Getestete mit einer 92-prozentigen Wahrscheinlichkeit erkrankt. Mit steigendem Krankheitsrisiko steigt also auch die Wahrscheinlichkeit an, bei positivem Testergebnis tatsächlich krank zu sein.
Für die Praxis bedeutet das, dass ein diagnostischer Test alleine oftmals nicht ausreicht, um eine „Ja“- oder „Nein“-Diagnose zu stellen. Auch die individuelle Situation der Getesteten und das Einschätzungsvermögen von Arzt oder Ärztin spielen eine wichtige Rolle bei der Diagnosestellung.
Text: Valérie Labonté, Harriet Sommer, Gabriel Torbahn
Bildnachweis Foto Malariaschnelltest: CDC Global via flickr unter CC-Lizenz
Für Interessierte: die Berechnung von Sensitivität, Spezifität und prädiktiven Werten
Die Test-Sensitivität lässt sich einfach berechnen, indem die Anzahl richtig positiver Testergebnisse durch die Summe aus richtig positiven und falsch negativen Testergebnissen geteilt wird. Als Hilfe dient eine klassische Vierfeldertafel:
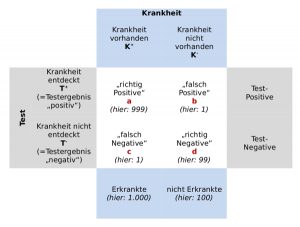
Die Formel zur Berechnung der Test-Sensitivität ist: a/(a+c), hier: 999/ (999 + 1) = 0,999 = 99,9 %. Die Test-Spezifität wird analog berechnet als Quotient aus richtig negativen und der Summe aus falsch positiven und richtig negativen Testergebnissen: d/b+d, hier: 99/(1+100) = 0,99 = 99 %.
Anmerkung: Die Zahlen aus dem Beispiel lassen sich natürlich nicht mit dem Test selbst bestimmen, sondern müssen vom Testhersteller ermittelt werden, indem zum Beispiel mit Referenztests verglichen wird.
Positive und negative Vorhersagewerte lassen sich mit Hilfe des Satzes von Bayes über bedingte Wahrscheinlichkeiten mit Sensitivität, Spezifität und Krankheitsprävalenz (PR) berechnen.
Positiver prädiktiver Wert: [Sens*PR]/[Sens*PR+(1–Spez)*(1–PR)],
negativer prädiktiver Wert: [Spez*(1–PR)]/[Spez*(1–PR)+(1–Sens)*PR].
Folgende Tabelle zeigt die errechneten positiven prädiktiven Werte (PPV oder „positive predictive value“) für verschiedene Prävalenzen (geringes, mittleres oder hohes Krankheitsrisiko) mit einer Sensitivität von 99,9 % und einer Spezifität von 99 %:

Man sieht schön, dass mit steigendem Krankheitsrisiko bzw. höherer Krankheitsprävalenz die Wahrscheinlichkeit, krank zu sein, in Form des positiven prädiktiven Wertes ansteigt.
Text: Harriet Sommer, Valérie Labonté, Gabriel Torbahn
Bildnachweis Vierfeldertafel und Tabelle: Harriet Sommer